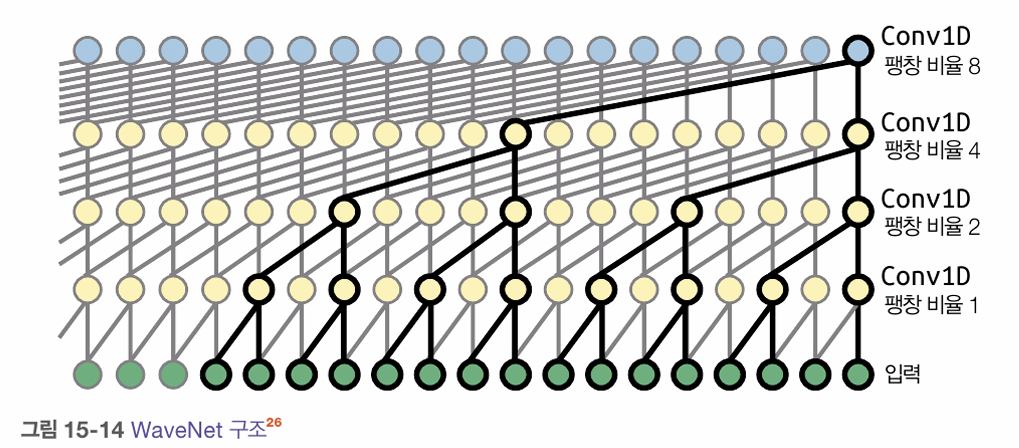
순환신경망(RNN)
- 미래를 예측할 수 있는 네트워크
- 시계열 데이터를 분석
- RNN이 순차 데이터를 다룰 수 있는 유일한 신경망은 아님.
- 순환 신경망은 피드포워드 신경망과 매우 비슷하지만 뒤쪽으로 순환하는 연결도 있다는 저머이 다름.

- 각 타임 스텝(프레임)마다 이 순환 뉴런은 x와 이전 타임 스텝의 출력인 ŷ 을 입력받음.
- 첫 번째 타임 스텝에서는 이전 출력이 없으므로 일반적으로 0으로 설정
- 오른쪽 그림처럼 시간을 축으로 표현한 것을 시간에 따라 네트워크를 펼쳤다고 말함.
- ❗ 타임스텝이란 순환 뉴런이 시간에 따라 한 번씩 연산을 수행하는 순간을 의미, 그림에서 x(n)

- 타임스텝 t마다 모든 뉴런은 입력 벡터 x와 이전 타임 스텝의 출력 벡터 ŷ을 받음.
- 이제 입력과 출력이 모두 벡터가 됨.
- 각 순환 뉴런은 두 벌의 가중치 가짐 하나는 입력 x를 위한 것 다른 하나는 타임 스텝 ŷ을 위한 것
- 이 가중치 벡터를 wₓ , w𝑦 라고 함.
식 및 기호 설명
메모리 셀

- 타임 스텝 t에서 순환 뉴런의 출력은 이전 타임 스텝의 모든 입력에 대한 함수이므로 일종의 메모리 형태
- 타임 스텝에 걸쳐서 어떤 상태를 보존하는 신경망의 구성요소를 메모리 셀이라 함..
- 하나의 순환 뉴런 또는 순환 뉴런의 층은 짧은 패턴만 학습할 수 있는 매우 기본적인 셀
- 일반적으로 타임 스텝 t에서의 셀의 상태 hₜ는 해당 타임 스텝의 입력과 이전 타임 스텝의 상태에 대한 함수
- 타임스텝 t에서의 출력 ŷ ₜ도 이전 상태와 현재 입력에 대한 함수
입력과 출력 시퀀스

- RNN - 입력 시퀀스를 받아 출력 시퀀스를 만드는 시퀀스-투-시퀀스 네트워크
- 시퀀스-투-벡터 네트워크 : 입력 시퀀스를 네트워크에 주입하고 마지막을 제외한 모든 출력을 무시
- 벡터-투-시퀀스 네트워크 : 각 타입 스텝에서 하나의 입력 벡터를 반복해서 네트워크에 주입하고 하나의 시퀀스를 출력
- 인코더-디코더 : 인코더라 부르는 시퀀스-투-벡터 네트워크 뒤에 디코더라 부르는 벡터-투-시퀀스 네트워크를 연결
RNN 훈련하기

- BPTT : RNN을 훈련하기 위한 기법, 타임 스텝으로 네트워크를 펼치고 보통의 역전파를 사용하는 것.
BPTT 단계
- 첫 번째 정방향 패스가 펼쳐진 네트워크를 통과하면서 진행됨.
- 손실 함수를 사용해 출력 시퀀스를 평가함.
- 여기서 는 타겟 값, 는 예측 값.
- 예를 들어, 시퀀스-투-벡터 RNN에서는 마지막 출력을 제외한 모든 출력이 무시됨.
- 손실 함수의 그래디언트는 펼쳐진 네트워크를 따라 역방향으로 전파됨.
- 출력은 손실 계산에서 제외되므로 그래디언트가 이 두 값을 통과하지 않음.
- 따라서 역방향으로 흐르지 않고 ŷ2, ŷ 3, ŷ 4를 통해서만 흘러감.
- 동일한 파라미터 w와 b가 사용되기 때문.
- 그레디언트는 역전파 ㄷ동안에 여러 번 조정될 것임.
- 역방향 계산이 완료되고 모든 그레디언트가 계산되면 BPTT는 경사 하강법 단계를 수행해 파라미터를 업데이트 할 수 있음.
- 시계열 : 일반적으로 일정한 간격의 타임스텝별 값을 가진 데이터
- 다변량 시계열 : 타임 스텝마다 여러 개의 값이 있음.
- 단변량 시계열 : 타임 스텝마다 한 개의 값이 있음.
- 정상 시계열 : 계절성이나 트렌드가 없어 시간에 따라 통계적 속성이 일정함.
- 주간 계절성 : 매주 비슷한 패턴이 반복되는 것
- 단순 예측 : 과거 값을 단순히 복사해 예측을 만듦.
- 차분 : 두 시계열간의 차이, 시계열에서 트렌드와 계절성 제거를 위해 사용하는 대표적인 기법
- 자기상관 시계열 : 시계열이 시간이 지연된 자기자신과 상관관계를 가짐
- 평균 절대 비율 오차 : 예측 오차를 타깃값으로 나눔.
ARMA 모델
- ARMA : 자기 회귀 이동 평균
- 지연된 값의 간단한 가중치 합을 사용해 예측을 구하고 이동 평균을 더해 예측을 수정, 구체적으로 마지막 몇 개의 예측 오차의 가중치 합을 사용해 이동 평균을 계산

- ⭐ 이 모델이 정상 시계열을 가정함.
- 한 타임 스텝에 대한 차분을 구하면 시계열의 도함수를 근사할 수 있음. 이는 실제로 각 타임 스텝에서 시계열의 기울기임. = 선형적인 트렌드를 제거하고 일정한 값으로 변환함.
- 누적 차수 : 연속적인 d번의 차분을 수행하면 시계열의 d차 도함수를 근사할 수 있음. d차 다항식 트렌드를 제거할 수 있음. 이 하이퍼파라미터 d를 의미
ARIMA
- 차분은 자기 회귀 누적 이동 평균(ARIMA)의 핵심임
- d번의 차분을 수행해 시계열을 정상 상태로 만들고 일반적인 ARMA 모델을 적용
- 예측을 수행할 때 ARMA 모델을 사용한 후 차분으로 뺐던 값을 다시 더함.
계절성 ARIMA
- ARIMA와 같은 방식으로 시계열을 모델링하지만 주어진 빈도에 대한 계절 항을 추가로 모델링
- 총 ㅇ7개의 하이퍼파라미터를 각짐.
- ARIMA 모델을 위한 p,d,q하이퍼파라미터, 계절성 패턴을 모델링하기위한 P,D,Q 하이퍼파라미터, 계절성 패턴의 간격인 s가 있음.
💡 SARIMA 모델의 하이퍼파라미터를 선택하는 방법
: 가장 이해하기 쉽고 시작하기 좋은 방법은 단순한 그리드 서치임.
심층 RNN으로 예측하기
- 위와 같이 셀을 여러 층으로 쌓아 만든 것
- 케라스로 심층 RNN을 구현하는 법 : 순환 층을 쌓기
여러 타임 스텝 앞 예측하기
- 타깃을 적절히 바꾸어 여러 타임 스텝 앞의 값을 손쉽게 예측할 수 있음.
- 방법이 두 가지 존재함.
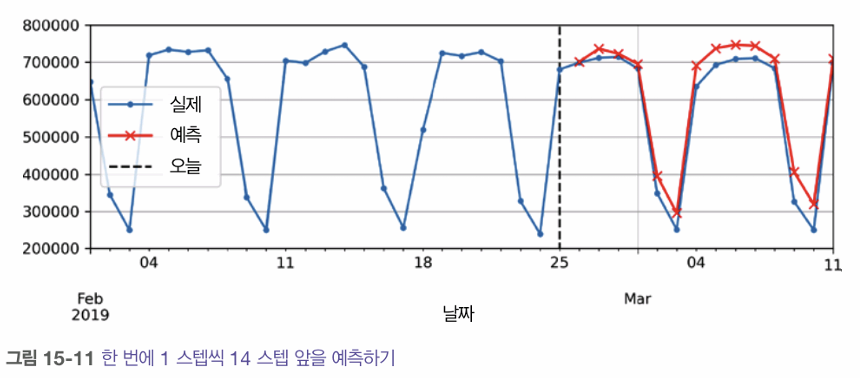
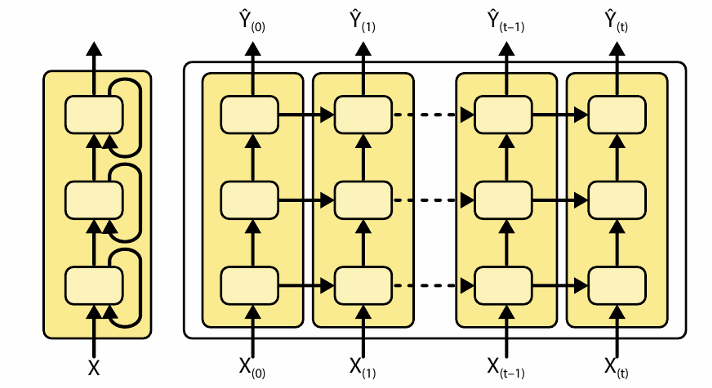
- 훈련된 모델을 사용해 다음 값을 예측한 다음, 예측된 값이 실제로 발견된 것처럼 입력으로 추가하는 것. 그리고 이 모델을 사용해 다시 다음 값을 예측하는 식. 모델을 사용해 반복적으로 다음 값을 예측하고 각 예측값을 시간축을 따라 입력 시계열에 덧붙이기.
- 한 번에 다음 (n)개 값을 예측하는 RNN 훈련하기. 다음 날에 대한 예측이 N일 후에 대한 예측보다 확실히 낫지만 이전 방식처럼 오차를 누적하지 앙ㄶ음.
시퀸스-투-시퀸스 모델로 예측하기
시퀸스-투-시퀸스 RNN
- 마지막 타임 스텝의 출력 뿐만 아니라 모든 타임 스텝의 RNN 출력이 손실에 포함됨. = 훨씬 많은 오차 그레디언트가 모델로 흘러감.
- 마지막 타임 스텝 뿐만 아니라 각 타임 스텝의 출력에서 오차 그레디언트가 나오기 때문에 시간을 거슬러 오래저너파되지 않아도 됨.
- 이는 훈련을 안정시키고 속도를 높임.
인과모델 : 매 타임 스텝마다 RNN은 과거 스텝에 대한 정보만 알고 있으며 앞을 내다볼 수 없음.
긴 시퀀스 다루기
1. 불안정한 그레디언트
- 불안정한 그레디언트 문제 완화를 위해 좋은 가중치 초기화, 빠른 옵티마이저, 드롭아웃 등 사용 가능.
- but 활성화 함수는 도움 x, 경사하강법이 출력을 조금 증가시키는 방향으로 가중치를 업데이트한다 할 때, 가중치가 타입 스텝마다 계속 증가하다가 출력이 폭주하기 때문. 수렴하지 않는 활성화 함수는 이를 막지 못함.
- 작은 학습률 사용 / tanh 함수 같이 수렴하는 활성화 함수를 사용해 이런 위험을 감소 시킬 수 있음.
- 같은 방식으로 그레디언트 자체도 폭주할 수 있음.
- 훈련이 불안정하다고 느껴지면 그레디언트의 크기를 모니터링하고 그레디언트 클리핑을 사용하는 것이 좋음.
💡 그레디언트 클리핑이란?
그레디언트 클리핑(Gradient Clipping)은 신경망 학습 과정에서 발생하는 기울기 폭발(Gradient Explosion) 문제를 방지하는 기법이다. 기울기의 크기가 특정 임계값을 초과하면 이를 강제로 제한하여 가중치 업데이트가 과도하게 이루어지는 것을 막는다. 일반적으로 L2 노름(norm)이나 절댓값 기준으로 클리핑을 수행하며, 이를 통해 학습의 안정성을 높일 수 있다. 특히 RNN, LSTM, GRU 같은 순환 신경망에서는 기울기 폭발이 자주 발생하기 때문에 이 기법이 매우 중요하다. 하지만 임계값을 너무 낮게 설정하면 학습이 느려질 수 있으므로, 적절한 값을 선택하는 것이 중요하다.
층 정규화
- RNN에 잘 맞는 다른 종류의 정규화는 층 정규화이다.
- 층 정규화는 배치 차원에 대해 정규화하는 대신 특성 차원에 대해 정규화 함.
- 샘플에 독립적으로 타임 스텝마다 동적으로 필요한 통계를 계산할 수 있음.
- 훈련과 테스트에서 동일한 방식으로 작동한다는 것 의미.
- 훈련 세트의 모든 샘플에 대한 특성 통계를 추정하기 위해 지수 이동 평균이 필요하지 않음.
- 입력마다 하나의 스케일과 이동 파라미터를 학습함.
- RNN에서 층 정규화는 일반적으로 입력과 은닉 생태의 선형 조합 직후에 사용됨.
LSTM 셀
- 장단기 메모리 셀
- 훈련이 빠르게 수렴하고 데이터에 있는 장기간의 의존성을 감지할 것
LSTM 작동방식
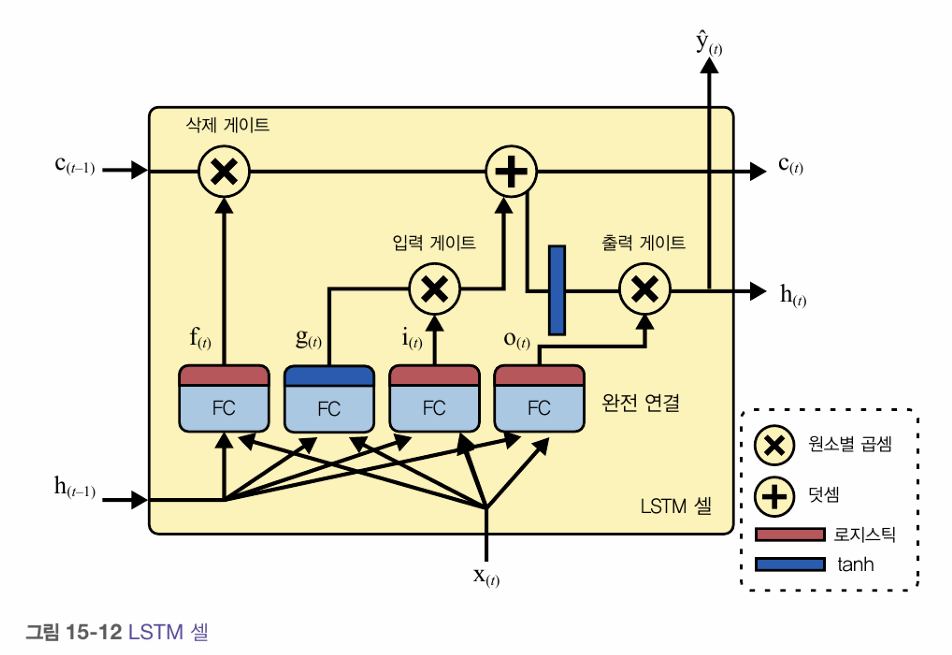
- 핵심 아이디어 - 네트워크가 장기 상태에 저장할 것, 버릿 것, 그리고 읽어들일 것을 학습하는 것
- 장기 기억 c는 네트워크를 왼쪽에서 오른쪽으로 관통하면서 삭제 게이트를 지나 일부 기억을 잃고, 덧셈 연산으로 새로운 기억을 추가함.
- 만들어진 c는 다른 추가 변환 없이 바로 출력으로 보내짐.
- 타임 스텝마다 일부 기억이 삭제되고 일부 기억이 추가됨.
- 덧셈 연산 후 이 장기 상태가 복사되어 tanh 함수로 전달 됨.
- 이 결과는 출력 게이트에 의해 걸러짐. 이는 단기 상태 h를 만듦.
상세 설명

하나의 샘플에 대해 타임 스텝마다 셀의 장기 상태와 단기 상태 그리고 출력을 계산하는 법


간단히 말해 LSTM 셀은 중요한 입력을 인식하고, 장기 상태에 저장하고, 필요한 기간 동안 이를 보존하고, 필요할 때마다 이를 추출하기 위해 학습함.
GRU 셀
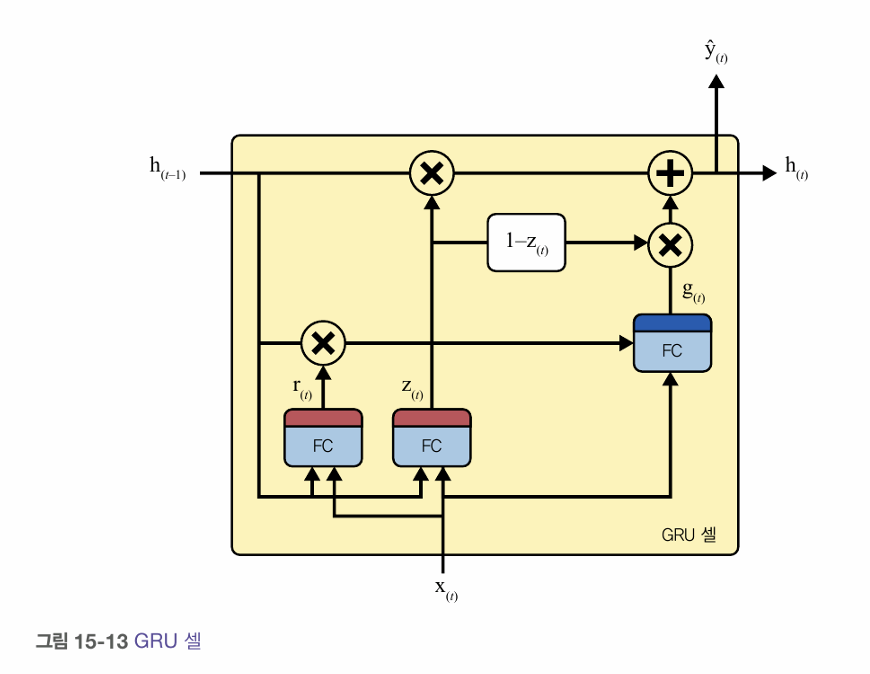
- 게이트 순환 유닛 셀
- LSTM 셀의 간소화된 버전이며 유사하게 작동하는 것처럼 보임.
간소화 내용

식

WaveNet
- 이 네트워크는 층마다 팽창 비율을 두 배로 늘리는 1D 합성곱 층을 쌓음.
- 첫 번째 합성곱 층이 한 번에 2개의 타임 스텝만 바라봄.
- 다음 층은 4개의 타임 스텝을 보고, 다음은 8개의 타임 스텝을 보는 식임.
- 하위 층은 단기 패턴을 학습하고 상위 층은 장기 패턴을 학습함.
- 팽창 비율을 두 배로 늘린 덕분에 네트워크는 아주 긴 시퀸스를 매우 효율적으로 처리할 수 있음.
- 여러 오디오 문제에서 최상의 성능을 달성