실전 데이터분석 1주차

7, 9장 바로가기

 

5장 사이파이를 사용한 기본 확률 및 통계 분석

 

예산이 제한된다면 데이터도 제한 될 수 밖에 없고, 데이터와 투입 가능한 자원 간 절충이 현대 통계의 핵심.

통계의 목적 : 데이터 크기가 제한된 경우에서도 데이터에서 숨겨진 의미를 찾는 것

 

5.1 사이파이로 데이터와 확률 간 관계 탐색하기

사이파이

from scipy import stats

• 과학적 파이썬의 줄인말
• 과학적 분석에 유용한 여러 기능을 제공
• 확률과 통계 문제 해결용으로 만들어진 전용 모듈 scipy.stats를 포함함
•  scipy.stats 모듈은 데이터의 임의성 평가에 매우 유용
• stats.binom_test 메서드 : 이항 분포, 확률을 측정할 수 있음.

 

num_heads = 16
num_flips = 20
prob_head = 0.5
prob = stats.binomtest(num_heads, num_flips, prob_head)
print(f"15개 이상의 동전 앞면 또는 뒷면이 관찰될 확률은 {prob.pvalue:.17f}입니다.")

 

• 정확히 앞면 16개가 관측될 확률을 구하려면 stats.binom.pmf 메서드를 사용해야한다.
• stats.binom.pmf 메서드는 이항 분포의 확률 질량 함수를 표현한다.
• 확률 질량 함수는 입력 정수 값들을 각 값들이 발생할 확률에 매핑한다.

 

 

 

prob_16_heads = stats.binom.pmf(num_heads, num_flips, prob_head)
print(f"{num_heads}번의 앞면 중 {num_flips}번이 관측될 확률은 {prob_16_heads}입니다.")

• 정확히 동전 앞면이 16번 관측될 확률 구하기 위해 stats.binom.pmf 메서드를 사용함.
• 하지만 이 메서드는 여러 확률을 동시에 계산할 수도 있다.

 

 

 

probabilities = stats.binom.pmf([4, 16], num_flips, prob_head)
assert probabilities.tolist() == [prob_16_heads] * 2

• stats.binom.pmf([4, 16], num_flips, prob_head)를 실행하면 동일한 두 요소를 가진 배열이 반환됨.
• 앞면 4번과 뒷면 16번을 관측할 확률 = 뒷면 4번, 앞면 16번을 볼 확률과 동일하기 때문임.

 

 

interval_all_counts = range(21)
probabilities = stats.binom.pmf(interval_all_counts, num_flips, prob_head)
total_prob = probabilities.sum()
print(f"확률의 총합은 {total_prob:.14f}입니다.")

• interval_all_counts에 따른 확률을 그래프로 나타내면 분포도를 얻을 수 있음.

 

import matplotlib.pyplot as plt
plt.plot(interval_all_counts, probabilities)
plt.xlabel('동전 앞면의 등장 횟수')
plt.ylabel('확률')
plt.show()

 

• stats.binom.pmf 메서드 덕분에 분포도를 시각화 할 수 있었다.

 

flip_counts = [20, 80, 140, 200]
linestyles = ['-', '--', '-.', ':']
colors = ['b', 'g', 'r', 'k']

for num_flips, linestyle, color in zip(flip_counts, linestyles, colors):
    x_values = range(num_flips + 1)
    y_values = stats.binom.pmf(x_values, num_flips, 0.5)
    plt.plot(x_values, y_values, linestyle=linestyle, color=color,
label=f'{num_flips} 회의 동전 뒤집기')

plt.legend()
plt.xlabel('동전 앞면의 등장 횟수')
plt.ylabel('확률')
plt.show()

 

 

• 각 이항 분포의 최대 확률 지점은 동전 뒤집기를 많이 시행할수록 오른쪽으로 이동함.
• 분포도 중심이 오른쪽으로 이동할수록 그들의 분포는 중심에서 더욱 분산되는 것을 알 수 있음.
• 이런 분포 차이를 정량화 할 필요가 있음.
• 중심성 및 분산에 구체적인 수치를 부여하여 분포도마다 각 수치가 변하는 방식을 파악해야함.

 

 

5.2 중심성의 척도로서 평균

 

import numpy as np
measurements = np.array([80, 77, 73, 61, 74, 79, 81])

• measurements.sort() 메서드를 호출해 측정값들을 순서대로 정렬
• 정렬된 측정치를 그래프로 나타내어 중심 값을 판단해볼 수 있음.

 

 

 

 

measurements.sort()
number_of_days = measurements.size
plt.plot(range(number_of_days), measurements)
plt.scatter(range(number_of_days), measurements)
plt.ylabel('온도')
plt.show()

• 중심온도가 대충 70도인 것을 추정 가능

 

 

difference = measurements.max() - measurements.min()
midpoint = measurements.min() + difference / 2
assert midpoint == (measurements.max() + measurements.min()) / 2
print(f"중간 온도는 {midpoint}도 입니다 ")

• 최저 온도와 최고 온도의 중앙값을 정량적으로 파악하는 방법은 최저 및 최고 온도 값을 더한 뒤 2로 나누어 얻거나 최고 온도에서 최저 온도를 뺀 뒤 다시 최저 온도를 더하는 방식으로 알 수 있음.

 

 

plt.plot(range(number_of_days), measurements)
plt.scatter(range(number_of_days), measurements)
plt.axhline(midpoint, color='k', linestyle='--')
plt.ylabel('온도')
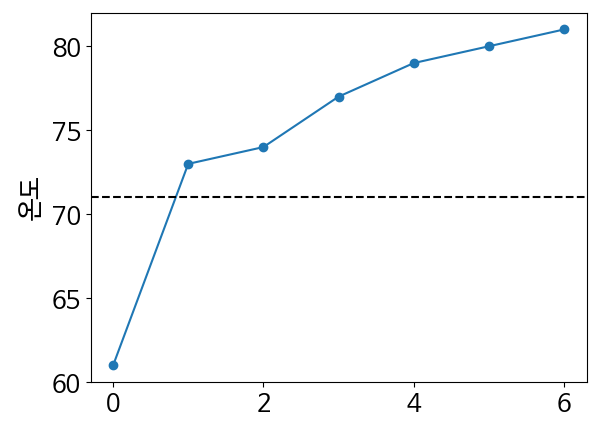
plt.show()

• 중앙값 : 측정치들을 균등하게 두 부분으로 나눌 수 있는 값을 말한다.
• 다음 그래프는 최저 및 최고 온도의 중간 값을 나타냄

 

 

median = measurements[3]
print(f"온도의 중앙값은 {median}도 입니다")
plt.plot(range(number_of_days), measurements)
plt.scatter(range(number_of_days), measurements)
plt.axhline(midpoint, color='k', linestyle='--', label='중간지점')
plt.axhline(median, color='g', linestyle='-.', label='중앙값')
plt.legend()
plt.ylabel('온도')
plt.show()

 

 

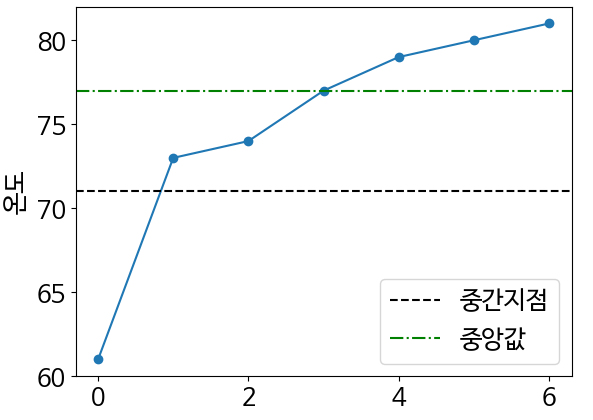
• 77도의 중앙값은 온도를 반으로 나누고, 장앙값은 낮은 온도 세 개보다 높은 온도 세 개에 더 가까워 균형이 맞지 않는 것처럼 보임.
• 여기에 페널티를 부여하면 이 불균형을 맞춰줄 수있음.

 

def squared_distance(value1, value2):
    return (value1 - value2) ** 2

possible_centers = range(measurements.min(), measurements.max() + 1)
penalties = [squared_distance(center, 61) for center in possible_centers]

plt.plot(possible_centers, penalties)
plt.scatter(possible_centers, penalties)
plt.xlabel('가능한 중앙값')
plt.ylabel('페널티')
plt.show()

 

• 페널티는 두 값 간의 차이를 제곱한 거리의 제곱으로 구현할 수 있음
• 거리의 제곱은 두 값이 멀어질수록 네 제곱으로 증가함.

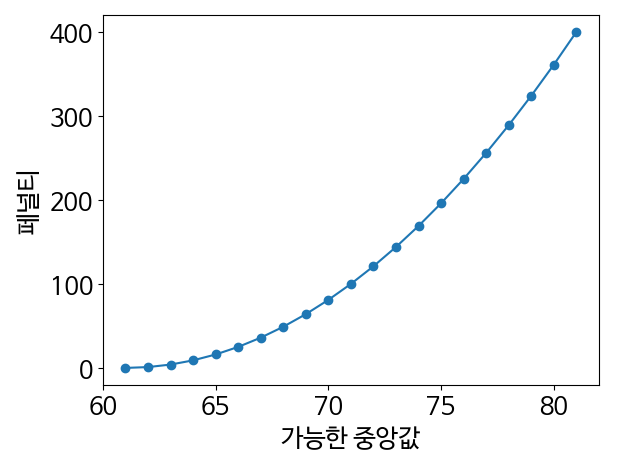
• 최솟값에서 떨어진 거리를 기준으로 가능한 중심 범위에 걸친 페널티를 보여줌

 

 

 

def sum_of_squared_distances(value, measurements):
    return sum(squared_distance(value, m) for m in measurements)

penalties = [sum_of_squared_distances(center, measurements)
    for center in possible_centers]

plt.plot(possible_centers, penalties)
plt.scatter(possible_centers, penalties)
plt.xlabel('가능한 중심값')
plt.ylabel('페널티')
plt.show()

• 측정치 일곱 개에 대한 제곱 거리를 기반으로 각 잠재적인 중심에 페널티를 부여해야함.
• 이를 위해 특정 값과 측정된 값들의 배열 간 제곱 거리를 모두 더하는 함수를 정의
• 이 함수가 새로 부여될 페널티를 결정할 것임.
• 가능한 중심과 페널티를 비교해 그래프를 그리면 페널티가 최소화되는 중심을 찾을 수 있음.

 

 

 

 

 

 

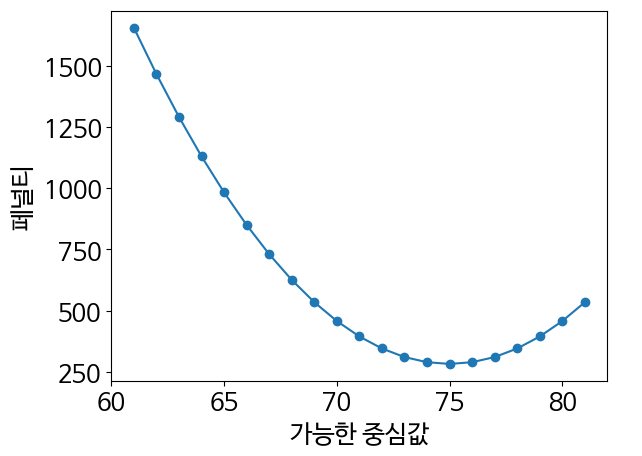
least_penalized = 75
assert least_penalized == possible_centers[np.argmin(penalties)]

plt.plot(range(number_of_days), measurements)
plt.scatter(range(number_of_days), measurements)
plt.axhline(midpoint, color='k', linestyle='--', label='중간지점')
plt.axhline(median, color='g', linestyle='-.', label='중앙값')
plt.axhline(least_penalized, color='r', linestyle='-', label='패널티가 가장 낮은 중심')
plt.legend()
plt.ylabel('온도')
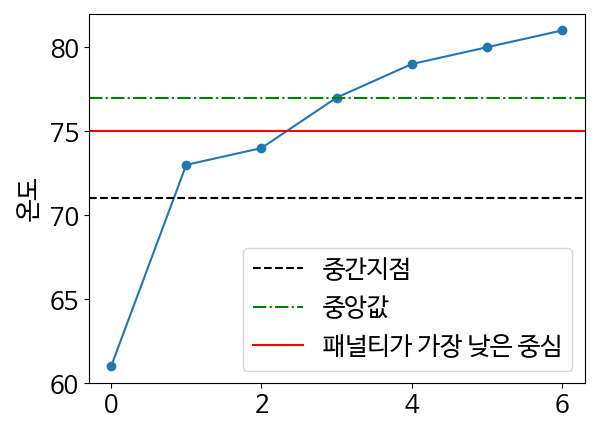
plt.show()

• 75도에 가장 낮은 페널티가 부여됨. 이를 페널티가 가장 낮은 중심이라 부르겠다.
• 여기서 저 페널티가 가장 낮은 중심은 중앙값에 비해 최저 온도에 더 가까운 거리를 제공하면서 동시에 데이터를 균형 있게 분할함.
• 페널티가 가장 낮은 중심은 중심성을 나타내는 좋은 척도이다.
• 중심과 모든 값 사이의 거리를 균형 잡히게 만들어 준다.

 

 

 

 

assert measurements.sum() / measurements.size == least_penalized

 

• 측정값을 모두 더한 뒤 배열 크기로 나누는 방식 → 페널티가 가장 낮은 중심을 바로 계산할 수 있음.

 

mean = measurements.mean()
assert mean == least_penalized
assert mean == np.mean(measurements)
assert mean == np.average(measurements)

• 배열 값들을 모두 더한 뒤 배열 크기로 나누는 것을 공식적으로 산술 평균이라고 함.
• 배열의 평균이라고도 함.
• 평균은 넘파이 배열의 mean 메서드를 호출하면 쉽게 계산할 수 있음.

 

 

equal_weights = [1] * 7
assert mean == np.average(measurements, weights=equal_weights)

unequal_weights = [100] + [1] * 6
assert mean != np.average(measurements, weights=unequal_weights)

 

• np.mean or np.average 메서드로 평균 계산할 수도 있음.
• np.mean과 np.average 메서드는 다름. 별도의 weights 라는 매개변수를 선택적으로 입력할 수 있기 때문
• 이 매개변수는 각 측정값이 다른 측정값에 비해 상대적으로 얼마나 중요한지 나타내는 가중치 리스트
• 모든 가중치가 균등하다면 np.mean와 np.average의 결과는 동일할 것이다.

 

weighted_mean = np.average([75, 77], weights=[9, 1])
print(f"평균은 {weighted_mean}입니다.")
assert weighted_mean == np.mean(9 * [75] + [77]) == weighted_mean

 

• 가중치 매개변수는 중복된 값들의 평균을 계산하는데 유용함.
• 중복된 값이 있는 상황에서 가중된 평균을 계산하면 일반적인 평균을 더 빠르게 얻을 수 있음.
• 고윳값들에 대한 상대적인 비율은 가중치 비율로 표현됨.

 

 

 

assert weighted_mean == np.average([75, 77], weights=[900, 100])
assert weighted_mean == np.average([75, 77], weights=[0.9, 0.1])

 

• 확률을 가중치로 취급할 수 있는 것. 따라서 어떤 확률 분포에서도 평균을 계산할 수 있다고 해석됨.

 

 

 

 

5.2.1 확률 분포의 평균 구하기

num_flips = 20
interval_all_counts = range(num_flips + 1)
probabilities = stats.binom.pmf(interval_all_counts, 20, prob_head)
mean_binomial = np.average(interval_all_counts, weights=probabilities)
print(f"이항 분포의 평균은 동전 앞면이 {mean_binomial:.2f}번 등장할 때입니다.")

plt.plot(interval_all_counts, probabilities)
plt.axvline(mean_binomial, color='k', linestyle='--')
plt.xlabel('동전의 앞면 수')
plt.ylabel('확률')
plt.show()

 

 

 

 

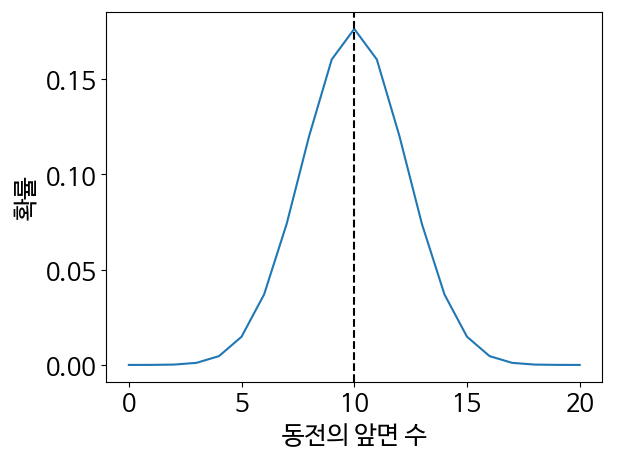
• 가장 높은 확률은 분포의 평균과 어떻게 다를까? np.average메서드의 가중치 매개변수에 확률들이 담긴 배열을 입력하면 평균을 구할 수 있음.
• 해당 평균을 분포를 가로지르는 수직선으로 그래프에 표현 가능
• 사이파이는 단순히 stats.binom.mean을 호출하는 것만으로도 모든 이항 분포의 평균을 쉽게 구함.
• stats.binom.mean 메서드를 호출할 때는 동전 뒤집기 횟수 및 동전 앞면이 나올 확률을 매개변수로 입력해야 함.

 

 

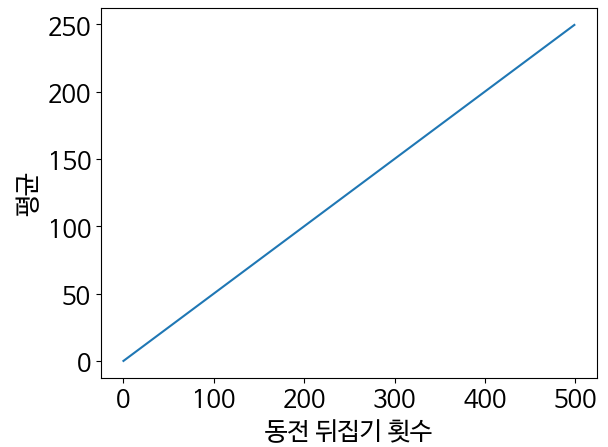
assert stats.binom.mean(num_flips, 0.5) == 10

• stats.binom.mean 메서드를 사용하면 이항 분포의 중심성과 동전 뒤집기 횟수 사이의 관계를 엄격히 분석 할 수 있음.

 

means = [stats.binom.mean(num_flips, 0.5) for num_flips in range(500)]
plt.plot(range(500), means)
plt.xlabel('동전 뒤집기 횟수')
plt.ylabel('평균')
plt.show()

 

• 동전 뒤집기 횟수와 분포 평균은 선형적인 관계
• 동전이 앞면으로 떨어질 균등한 확률은 베르누이 분포의 평균과 같음.

 

 

 

 

num_flips = 1
assert stats.binom.mean(num_flips, 0.5) == 0.5

 

 

 

 

num_flips = 1000
assert stats.binom.mean(num_flips, 0.5) == 500

interval_all_counts = range(num_flips)
probabilities = stats.binom.pmf(interval_all_counts, num_flips, 0.5)
plt.axvline(500, color='k', linestyle='--')
plt.plot(interval_all_counts, probabilities)
plt.xlabel('동전의 앞면 수')
plt.ylabel('확률')
plt.show()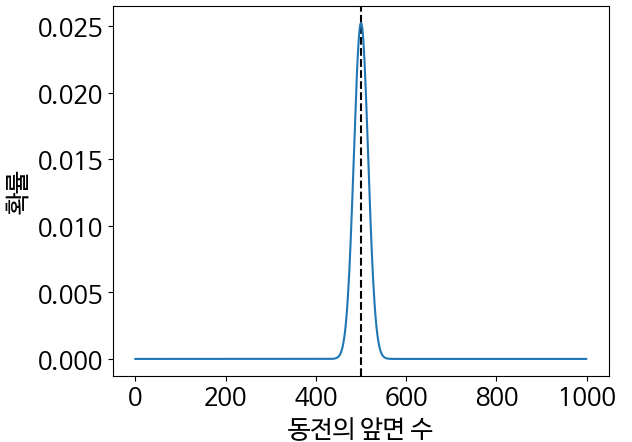

 

• 관측된 선형 관계를 사용하면 동전을 1000번 뒤집은 분포의 평균을 예측할 수 있음.

 

 

 

5.3 흩어진 정도를 측정하는 분산

• 흩어짐은 일부 중심 값 주변에 데이터가 흩어진 것을 의미
• 흩어진 정도가 작을수록 데이터에 대한 예측 가능성이 높아짐.
• 반면 흩어진 정도가 크다면 데이터의 출렁거림이 심할 것임.
• 캘리포니아주와 켄터키주의 여름 기온을 측정하는 시나리오 가정

 

california = np.array([52, 77, 96])
kentucky = np.array([71, 75, 79])

print(f"캘리포니아 주의 평균 온도는 {california.mean()}입니다.")
print(f"켄터키 주의 평균 온도는 {california.mean()}입니다.")

 

• 각 주의 평균 온도

 

 

plt.plot(range(3), california, color='b', label='캘리포니아')
plt.scatter(range(3), california, color='b')
plt.plot(range(3), kentucky, color='r', linestyle='-.', label='켄터키')
plt.scatter(range(3), kentucky, color='r')
plt.axhline(75, color='k', linestyle='--', label='평균')
plt.legend()
plt.show()

 

 

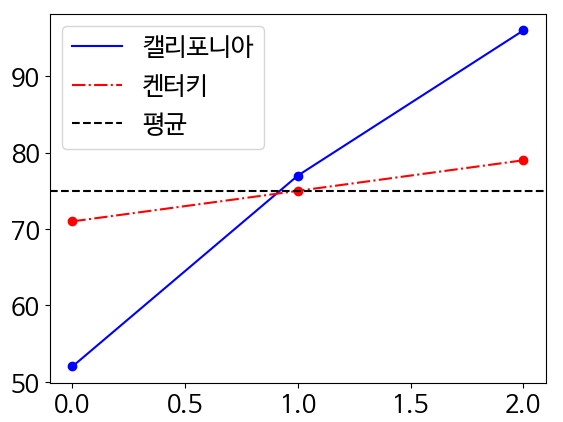
• 두 측정 배열을 그래프로 표현해 이러한 분산 차이를 시각화
• 수평선을 그려서 평균도 구분

 

def sum_of_squares(data):
    mean = np.mean(data)
    return sum(squared_distance(value, mean) for value in data)

california_sum_squares = sum_of_squares(california)
print(f"캘리포니아 온도의 제곱합은 {california_sum_squares}입니다.")

• 측정된 값과 평균 사이의 제곱 거리 합을 계산
• 평균에서 거리의 제곱합을 단순히 제곱합이라 함.
• 따라서  sum_of_squares라는 함수를 정의 이를 캘리포니아주에서 측정된 온도에 적용

 

kentucky_sum_squares = sum_of_squares(kentucky)
print(f"켄터키 온도의 제곱합은 {kentucky_sum_squares}입니다.")

 

• 캘리포니아주의 제곱합은 974가 나옴.
• 켄터키는 32가 나옴.
• 제곱합은 이 흩어진 정도를 측정하는 데 유용함. 다만 측정이  완벽하지는 않음.

 

 

california_duplicated = np.array(california.tolist() * 2)
duplicated_sum_squares = sum_of_squares(california_duplicated)
print(f"복제된 캘리포니아 온도의 제곱합은 {duplicated_sum_squares}입니다.")
assert duplicated_sum_squares == 2 * california_sum_squares

• 배열 복제 후 제곱합으로 계산

 

 

value1 = california_sum_squares / california.size
value2 = duplicated_sum_squares / california_duplicated.size
assert value1 == value2

• 제곱합은 입력된 배열 크기에 영향을 받기에 흩어진 정도를 측정하기 좋은 수단은 아님.
• 하지만 다행히 배열 크기로 제곱합을 나누어 이러한 영향을 쉽게 제거 가능함.

 

 

def variance(data):
    mean = np.mean(data)
    return np.mean([squared_distance(value, mean) for value in data])

assert variance(california) == california_sum_squares / california.size

 

• 제곱을 측정된 배열 크기로 나누는 것 = 분산임
• 분산 : 평균으로부터의 평균 제곱 거리

 

assert variance(california) == variance(california_duplicated)

 

 

 

california_variance = variance(california)
kentucky_variance = variance(kentucky)
print(f"캘리포니아의 온도에 대한 분산은 {california_variance}입니다.")
print(f"켄터키의 온도에 대한 분산은 {kentucky_variance}입니다.")

• 분산은 흩어진 정도를 측정하기 좋은 수단임.
• 파이썬 리스트 또는 넘파이 배열에 대해 np.var 함수를 호출하면 쉽게 계산 가능
• 넘파이 배열을 사용할 때는 내장된 var 메서드로도 계산 가능

 

 

assert california_variance == california.var()
assert california_variance == np.var(california)

• 분산은 평균에 따라 달라짐 가중된 평균을 계산한다면 분산 또한 가중된 분산을 계산해야함.
• 가중된 분산은 단순히 가중된 평균으로부터의 모든 거리 제곱의 평균을 계산하면 구할 수 있음.

 

 

def weighted_variance(data, weights):
    mean = np.average(data, weights=weights)
    squared_distances = [squared_distance(value, mean) for value in data]
    return np.average(squared_distances, weights=weights)

assert weighted_variance([75, 77], [9, 1]) == np.var(9 * [75] + [77])

 

• 데이터 리스트와 가중치를 매개변수로 입력받으며, np.average 함수로 평균으로부터의 거리 제곱에 대한 가중 평균을 계산

 

 

5.3.1 확률 분포의 분산 구하기

공정하게 20번 시행한 동전 뒤집기에 대한 이항분포의 분산을 계산해보자.

 

 

interval_all_counts = range(21)
probabilities = stats.binom.pmf(interval_all_counts, 20, prob_head)
variance_binomial = weighted_variance(interval_all_counts, probabilities)
print(f"이항 분포의 분산은 동전 앞면이{variance_binomial:.2f}번 등장했을 때입니다")

• 이항 분포의 분산은 5, 이는 이항 분포 평균의 절반에 해당
• 사이파이의 stats.binom.var 함수를 사용하면 이 분산을 더욱 빠르고 직접적으로 계산 가능

 

 

 

assert stats.binom.var(20, prob_head) == 5.0
assert stats.binom.var(20, prob_head) == stats.binom.mean(20, prob_head) / 2

•  stats.binom.var함수를 사용하면 이항 분포의 흩어진 정도와 동전을 뒤집은 횟수 사이의 관계를 엄격히 분석할 수 있음.

 

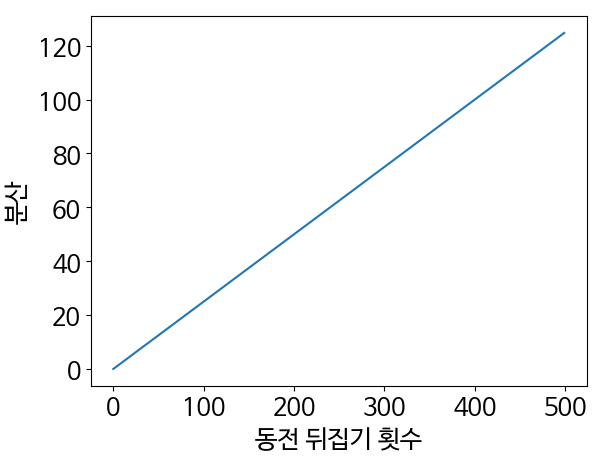
stats.binom.var(num_flips, prob_head)

 

 

 

variances = []

for num_flips in range(500):
    variances.append([stats.binom.var(num_flips, prob_head)])

plt.plot(range(500), variances)
plt.xlabel('동전 뒤집기 횟수')
plt.ylabel('분산')
plt.show()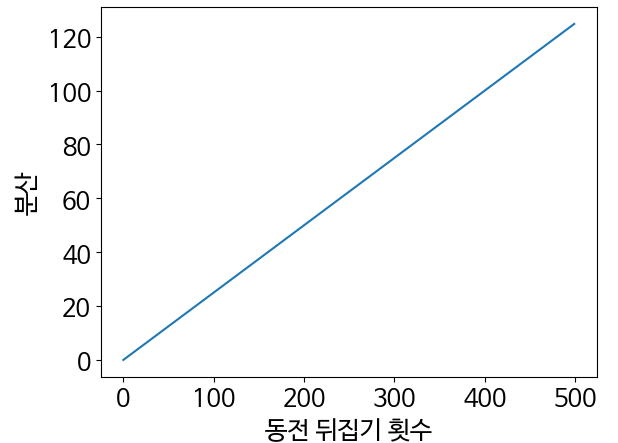

 

 

assert stats.binom.var(1, 0.5) == 0.25
assert stats.binom.var(1000, 0.5) == 250

 

• 분산은 동전 뒤집기 횟수의 1/4에 해당, 따라서 동전을 뒤집기 횟수가 1인 베르누이 분포의 분산은 0.25

 

 

 

data = [1, 2, 3]
standard_deviation = np.std(data)
assert standard_deviation ** 2 == np.var(data)

 

• 표준 편차는 분산의 제곱근임, np.std 함수로 쉽게 계산 가능하다.
• 이를 제곱하면 다시 분산을 얻을 수 있다
• 단위를 더 쉽게 추적하는 수단으로 분산 대신 표준 편차를 많이 사용한다.
• 평균과 표준 편차는 매우 유용한 값으로 수치형 데이터셋비교/확률분포 비교/ 수치형 데이터셋과 확률 분포 비교 등 가능하다.

 

 

 

6장 사이파이와 중심 극한 정리로 예측하기

• 정규 분포는 3장에서 소개된 종 모양의 곡선
• 중심 극한 정리 때문에 임의의 데이터 샘플링에서 자연스럽게 발생하는 것
• 반복적으로 샘플링된 빈도가 정규 분포 곡선의 모양을 만들어 낸다
• 이 정리는 각 빈도 표본의 크기가 커질수록 곡선의 폭은 좁아진다고 예측함.
• 분포의 표준 편차는 표본 크기가 증가할수록 줄어든다.

 

 

6.1 사이파이로 정규 분포 다루기

• 표본은 배열을 가지고, 배열 길이는 표본 크기이다.
• 동전 뒤집기 샘플에 대한 히스토그램을 그려 정규 분포 곡선을 생성해 보자.

 

 

np.random.seed(0)
sample_size = 10000
sample = np.array([np.random.binomial(1, 0.5) for _ in range(sample_size)])
head_count = sample.sum()
head_count_frequency = head_count / sample_size
assert head_count_frequency == sample.mean()

 

• 임의의 단일 샘플에 대한 동전 앞면 빈도를 계산하고 그 빈도와 평균의 관계를 확인

 

 

 

 

np.random.seed(0)
frequencies = np.random.binomial(sample_size, 0.5, 100000) / sample_size

 

• 샘플 10만 번에 대한 동전 앞면 빈도를 코드 한 줄로 계산 할 수도 있다.

 

 

 

 

sample_means = frequencies
likelihoods, bin_edges, _ = plt.hist(sample_means, bins='auto', edgecolor='black', density=True)

plt.xlabel('구간별 샘플 평균')
plt.ylabel('상대적 확률')
plt.show()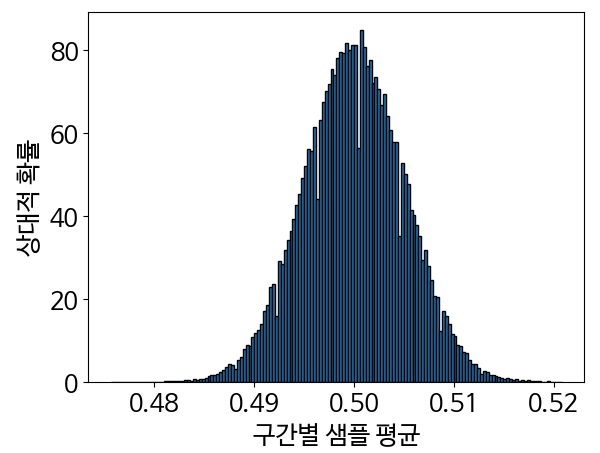

 

• 히스토그램을 이용해 sample_means에 담긴 데이터를 시각화
• 히스토그램이 정규 분포와 같은 모양을 띄는 것을 알 수 있음

 

 

mean_normal = np.average(bin_edges[:-1], weights=likelihoods)
var_normal = weighted_variance(bin_edges[:-1], likelihoods)
std_normal = var_normal ** 0.5
print(f"평균은 약 {mean_normal:.2f}입니다.")
print(f"표준 편차는 약 {std_normal:.3f}입니다.")

• 해당 분포의 평균과 표준 편차를 계산함.

 

 

import math
peak_x_value = bin_edges[likelihoods.argmax()]
print(f"평균은 약 {peak_x_value:.2f}입니다.")
peak_y_value = likelihoods.max()
std_from_peak = (peak_y_value * (2* math.pi) ** 0.5) ** -1
print(f"표준 편차는 약 {std_from_peak:.3f}입니다.")

• 분포의 평균은 약 0.5, 표준 편차는 0.005이다.
• 정규 분포에서 이 값들은 분포의 가장 높은 지점을 통해 즉시 계산될 수 있음.

 

 

 

fitted_mean, fitted_std = stats.norm.fit(sample_means)
print(f"평균은 약 {fitted_mean:.2f}입니다.")
print(f"표준 편차는 약 {fitted_std:.3f}입니다.")

• 평균과 표준 편차는 stats.norm.fit(sample_means)를 호출해 간단히 계산할 수 있음.
• 주어진 데이터로 형성된 정규 분포를 다시 생성할 수 있는 두 값을 반환한다.

 

 

 

 

normal_likelihoods = stats.norm.pdf(bin_edges, fitted_mean, fitted_std)
plt.plot(bin_edges, normal_likelihoods, color='k', linestyle='--', label='정규 확률 곡선')
plt.hist(sample_means, bins='auto', alpha=0.2, color='r', density=True)
plt.legend()
plt.xlabel('샘플 평균')
plt.ylabel('상대적 확률')
plt.show()

• stats.norm.pdf() 함수로 상대적 확률을 계산한 뒤 샘플링된 동전 뒤집기의 히스토그램과 함께 그래프로 표현

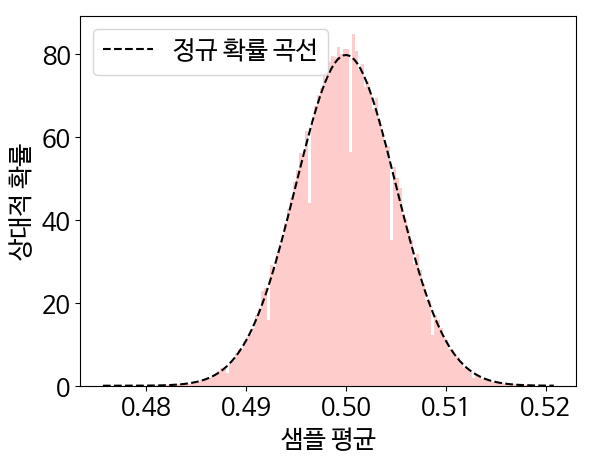
• 계산된 평균 및 표준 편차를 이용하면 정규 분포 곡선을 재현할 수 있음
• 간단히 stats.norm.pdf(bin_edges, fitted_mean, fitted_std)를 호출하기만 하면 됨.
• 사이파이의 stats.norm.pdf() 함수는 정규 분포의 확률 밀도 함수를 나타냄
• 확률밀도 함수는 확률 질량 함수와 유사하지만 확률을 반환하지 않는다는 주요 차이점이 있음. 그 대신 상대적 확률을 반환함.

 

 

 

adjusted_likelihoods = stats.norm.pdf(bin_edges, fitted_mean + 0.01, fitted_std / 2)
plt.plot(bin_edges, adjusted_likelihoods, color='k', linestyle='--')
plt.hist(sample_means, bins='auto', alpha=0.2, color='r', density=True)
plt.xlabel('샘플 평균')
plt.ylabel('상대적 확률')
plt.show()

 

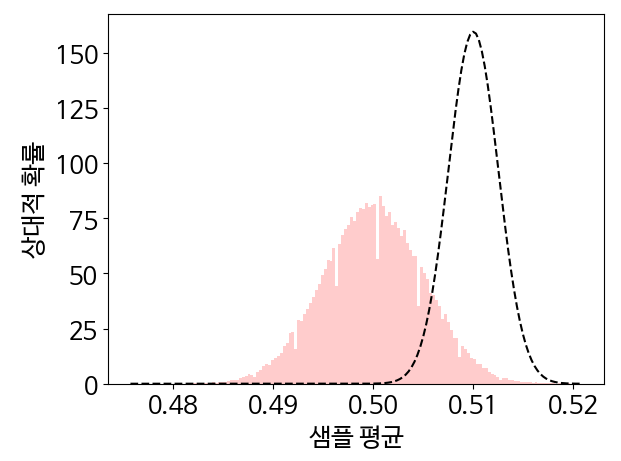
• 해당 최대 지점의 x,y좌표는 fitted_mean 및 fitted_std 함수의 결과와 같음.
• 최대 지점을 오른쪽으로 0.001 만큼 이동, 그 크기를 늘리는 예시가 위의 코드
• 입력 평균을 fitted_mean+0.01로 조정, 높이는 표준편차에 반비례하기 때문에 fitted_std /2  로 최대 지점에서 높이의 2배를 얻을 수 있음.

 

 

6.1.1 샘플링된 정규 분포 곡선 두 개 비교하기

 

 

np.random.seed(0)
new_sample_size = 40000
new_head_counts = np.random.binomial(new_sample_size, 0.5, 100000)
new_mean, new_std = stats.norm.fit(new_head_counts / new_sample_size)
new_likelihoods = stats.norm.pdf(bin_edges, new_mean, new_std)
plt.plot(bin_edges, normal_likelihoods, color='k', linestyle='--', label='A: 샘플 수 10K')
plt.plot(bin_edges, new_likelihoods, color='b', label='B: 샘플 수 40K')
plt.legend()
plt.xlabel('샘플 평균')
plt.ylabel('상대적 확률')
plt.show()

• 사이파이를 사용하면 입력된 매개변수를 바탕으로 정규 분포 모양을 탐색, 조정할 수 있음
• 입력 매개변수의 값은 임의의 데이터를 샘플링하는 방식에 따라 다름.
• 정규 분포의 전(A) 후(B) 모양을 그래프로 그려 비교함.

 

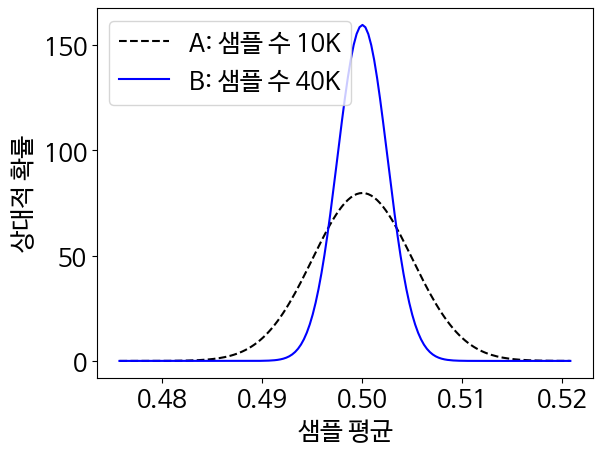
• 두 정규 분포의 중심 = 평균인 0.5 부근
• 표본 수가 더 많은 분포가 중심에서 더 좁게 퍼져 있음. = 표본 수가 증가함에 따라 최대 지점의 위치는 일정하게 유지되는 반ㅁ면 그 주변 영역의 폭은 줄어드는 것 관측 가능함.
• 최대 지점에 따라 퍼진 영역이 좁아지면 신뢰 구간은 감소함.
• 신뢰 구간 : 동전 앞면에 대한 실제 확률을 포함한 가능한 값 범위
• 표본 평균을 사용 시 동전 앞면의 확률을 구할 수 있음.

 

 

 

mean, std = new_mean, new_std
start, end = stats.norm.interval(0.95, mean, std)
print(f"이항 분포로 샘플링된 참 평균은 {start:.3f}와 {end:.3f} 사이에 있습니다")

• 정규 분포 B를 사용해 참 베르누이 평균에 대한 95% 신뢰 구간을 계산함
• 사이파이의 stats.norm.interval(0.95, mean, std)를 호출하면 그 범위를 자동으로 추출할 수 있다.
• 이 함수는 평균 및 표준 편차로 정의되는 정규 분포의 95% 영역을 포함하는 구간을 반환함.

 

 

 

 

assert stats.binom.mean(1, 0.5) == 0.5

 

• 정규 분포 곡선을 바탕으로 베르누이 분포의 분산을 추정함.
• 분포 A의 최대 지점 높이가 분포 B보다 약 2배 더 큼, 이 높이는 표준 편차에 반비례하므로 분포 B의 표준 편차는 분포 A의 표준 편차를 반으로 나눈 것과 같음.
• 표준 편차는 분산에 제곱근을 씌운 것, 분포 B 분산이 분포 A 분산의 1/4 이라는 것 유추 가능

 

 

 

variance_ratio = (new_std ** 2) / (fitted_std ** 2)
print(f"분산의 비율은 약 {variance_ratio:.2f}입니다")

• 실제로 분산의 비율을 출력해보면 0.25라고 나오는 것 확인 가능하다.

 

 

 

 

np.random.seed(0)
reduced_sample_size = 2500
head_counts = np.random.binomial(reduced_sample_size, 0.5, 100000)
_, std = stats.norm.fit(head_counts / reduced_sample_size)
variance_ratio = (std ** 2) / (fitted_std ** 2)
print(f" 분산의 비율은 약 {variance_ratio:.1f}입니다")

 

• 분산이 표본 크기에 반비례하는 것으로 보임.
• 위 코드 실행 시 분산의 비율 = 4.0인 것을 확인 가능.

 

 

 

 

estimated_variance = (fitted_std ** 2) * 10000
print(f"샘플 크기가 1인 경우, 추정 분산은 {estimated_variance:.2f} 입니다")

 

• 표본 크기가 4배 감소 시 분산은 4배 증가함.

 

 

 

 

assert stats.binom.var(1, 0.5) == 0.25

 

• 표본 크기 1에 대한 예측 분산 확인

 

 

정규 분포를 사용해 샘플링한 베르누이 분포의 분산과 평균을 계산하고 결과를 도출하는 과정

1. 베르누이 분포에서 무작위로 1과 0을 샘플링
2. sample_size 1과 0의 각 시퀀스를 단일 샘플로 그룹화
3. 모든 표본의 평균을 계산
4. 표본 평균은 정규 곡선을 생성
5. 평균과 표준 편차 구함
6. 정규 곡선의 분산에 표본 크기를 곱했을 때 베르누이 분포의 분산과 같았음.

 

다른 분포 사용하는 경우

• 푸아송 분포 : 시간당 스토어 방문 고객 수 , 초당 온라인 광고 클릭 수
• 감마 분포 : 한 지역의 월별 강우량, 대출 규모에 따른 은행 대출 불이행 건수
• 로그 정규 분포 : 주가 변동, 전염병의 잠복기

정규 곡선을 샘플링한 뒤에는 이를 사용해 기본 분포를 분석할 수 있음.

정규 곡선의 평균은 기본 분포의 평균에 근사함.

정규 곡선의 분산에 표본 크기를 곱하면 기본 분포의 분산에 근사치가 됨.

 

 

 

 

6.2 무작위 샘플링으로 모집단의 평균 및 분산 결정하기

np.random.seed(0)
population_ages = np.random.randint(1, 85, size=50000)

• 마을의 인구 수가 5만이라 할 때 한 마을에 사는 사람들의 평균 나이를 구하는 작업이 주어졌을 때.

 

 

population_mean = population_ages.mean()
population_variance = population_ages.var()

• 마을의 인구 평균과 인구 분산을 빠르게 계산해봄
• 그런데 실제로 얻어야하는 데이터가 엄청나게 많다면?

 

 

np.random.seed(0)
sample_size = 10
sample = np.random.choice(population_ages, size=sample_size)
sample_mean = sample.mean()

• 간단히 평균을 구할 수 있는 방법 = 마을에서 무작위로 사람들을 열 명 선정해 인터뷰하는 것
• np.random.choice 메서드에서 무작위로 열 명의 나이를 추출
• np.random.choice(population_ages, size=sample_size)를 실행하면 무작위로 샘플링된 나이 배열을 열 개 반환함.
• 샘플링이 완료되면 결과 요소 열 개로 구성된 배열 평균을 계산함.

 

 

 

percent_diff = lambda v1, v2: 100 * abs(v1 - v2) / v2
percent_diff_means = percent_diff(sample_mean, population_mean)
print(f"평균에 대해 {percent_diff_means:.2f}%의 차이가 있습니다.")

• 표본 평균과 모집단 평균을 비교했을 때.표본 평균과 모집단 평균 사이에 약 27% 차이가 있음.
• 표본이 충분치 않아 더 많은 표본을 수집해야함.
• 지원자들이 각각 인터뷰를 해서 데이터를 가져오는 병렬 느낌? 으로 진행하면 빠르게 많은 데이터를 수집 가능할 것이다.

 

 

 

 

np.random.seed(0)
sample_means = [np.random.choice(population_ages, size=sample_size).mean() for _ in range(100)]

• 1000명의 표본 평균을 계산한 것.
• 중심 극한 정리에 따르면, 표본 평균의 히스토그램은 정규 분포와 유사해야한다.
• 정규 분포 평균은 모집단 평균에 가까워야 한다.
• 표본 평균을 정규 분포에 맞추면 이것이 사실임을 확인 가능하다.

 

 

 

 

likelihoods, bin_edges, _ = plt.hist(sample_means, bins='auto', alpha=0.2, color='r', density=True)
mean, std = stats.norm.fit(sample_means)
normal_likelihoods = stats.norm.pdf(bin_edges, mean, std)
plt.plot(bin_edges, normal_likelihoods, color='k', linestyle='--')
plt.xlabel('샘플 평균')
plt.ylabel('상대적 확률')
plt.show()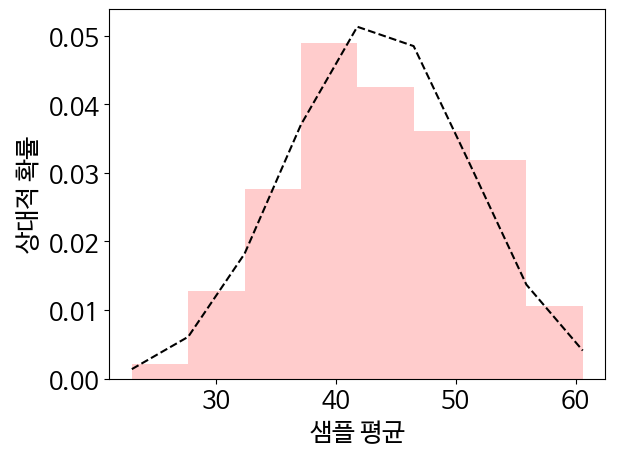

• 히스토그램은 데이터 포인트를 100개만 처리했기에 매끄럽지 않음.

 

 

 

 

print(f"실제 모집단 평균은 약 {population_mean:.2f} 입니다.")
percent_diff_means = percent_diff(mean, population_mean)
print(f"평균에 대해 {percent_diff_means:.2f}% 차이가 있습니다.")

• 그렇지만 히스토그램 모양은 여전히 정규 분포에 가까움. 이 분포 평균을 인쇄해 모집단 평균과 비교

 

 

 

 

normal_variance = std ** 2
estimated_variance = normal_variance * sample_size

• 표준 편차를 제곱하면 분포의 분산을 구할 수 있음. 이 분산을 이용하여 마을의 나이 분산을 추정할 수 있음.
• 계산된 분산에 표본 크기를 곱하기만 하면 됨.

 

 

 

print(f"추정 분산은 약 {estimated_variance:.2f} 입니다.")
print(f"실제 모집단 분산은 약 {population_variance:.2f} 입니다.")
percent_diff_var = percent_diff(estimated_variance, population_variance)
print(f"분산에 대해 {percent_diff_var:.2f}% 차이가 있습니다.")

• 추정분산 = 576.73, 모집단 분산 584.33, 분산 간 차이는 1.3% 이다.
• 분산이 비교적 정확하게 추정된 것을 확인 가능해졌다.

 

 

6.3 평균과 분산을 이용하여 예측하기

 

• 만 선생님이 25년간 5학년 학생들을 가르쳤고, 총 500명을 지도했다고 가정한다.
• 각 학생의 성적은 매년 학업 평가 시험으로 측정되며, 0점에서 100점까지 점수가 매겨짐.
• 데이터베이스에는 각 시험의 연도나 시험 회차 정보가 없어 특정 시험 성적을 직접 비교하기는 어렵습니다.

 

 

가정

 

선생님이 과거에 평균 성적이 89% 이상인 학급을 가르친 적이 있었는가?

• 이를 위해 데이터베이스를 조회한다고 가정한다.
• 과거 학생들의 개별 성적은 알 수 없지만, 전체 500명의 평균은 84점, 분산도 주어졌다고 가정한다.
• 이 값들(모집단 평균과 분산)을 바탕으로 선생님이 가르친 학급이 예외적으로 성적이 높은 집단인지 예측해보자는 내용.

 

population_mean = 84
population_variance = 25

 

• 모집단 평균은 84
• 모집단 분산은 25라고 할때

 

 

 

mean = population_mean
population_std = population_variance ** 0.5
sem = population_std / (20 ** 0.5)
grade_range = range(101)
normal_likelihoods = stats.norm.pdf(grade_range, mean, sem)
plt.plot(grade_range, normal_likelihoods)
plt.xlabel('20명 학생의 평균 성적 (%)')
plt.ylabel('상대적 확률')
plt.show()

• 평균 표준 오차 : 분산의 제곱근을 구하면 나오는 곡선의 표준 편차
• 평균 표준 오차는 모집단 표준 편차를 표본 크기의 제곱근으로 나눈 값과 같음.
• 곡선 매개변수를 계산하고 정규 곡선을 그림

 

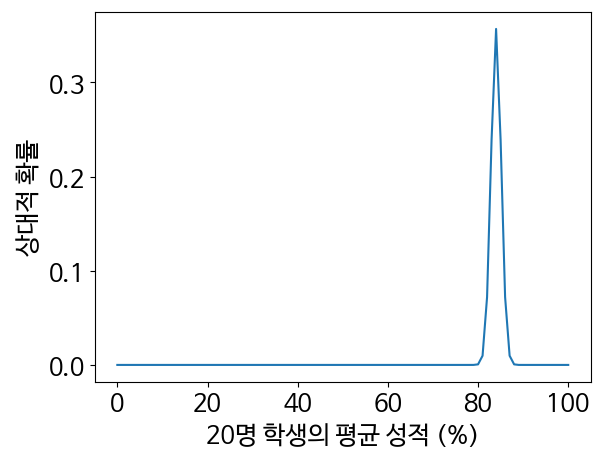
• 표시된 곡선 아래 면적은 89%에보다 높은 값에서 0에 가까워짐.
• 이 면적은 주어진 관측치 확률과도 같지만, 90% 이상 평균 성적이 관측될 확률은 매우 낮음.
• 확실히 하려면 실제 확률을 계산해야함.

 

 

 

6.3.1 정규 곡선 아래 면적 계산하기

• 법선 곡선은 직사각형으로 분해되지 않음.
• 한 가지 해결책 : 법선 곡선을 작은 사다리꼴 단위로 세분화하는 것 = 사다리꼴 규칙

 

total_area = np.sum([normal_likelihoods[i: i + 2].sum() / 2 for i in range(normal_likelihoods.size - 1)])
assert total_area == np.trapz(normal_likelihoods)
print(f"곡선 아래 예상 면적은 {total_area}입니다.")

• 사다리꼴 규칙을 정규 분포에 적용한 것

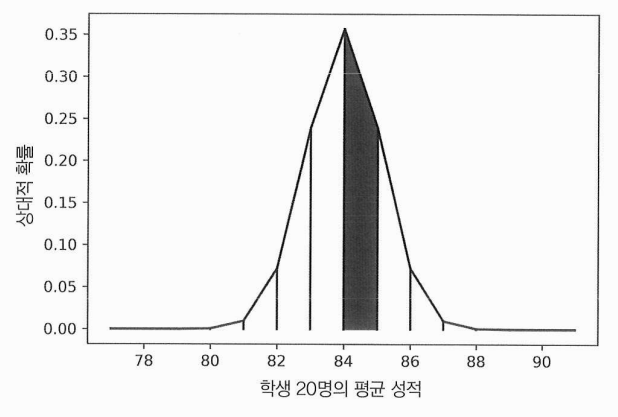
• 예상 면적은 1.0에 매우 가깝지만 정확히 1.0과 같지는 않다. 살짝 더 큼.
•  

 

 

 

assert stats.norm.sf(0, mean, sem) == 1.0

 

• 정확한 계산이 필요하다. 
• stats.norm.sf 메서드를 사용해 수학적으로 정확한 솔루션에 접근할 수 있다.
• 이 방법은 정규 곡선의 생존 함수를 나타냄.
• 즉, 생존 함수는 np.trapz(normal_likelihoods[mean:])로 근사한 면적에 대한 정확한 해법임.

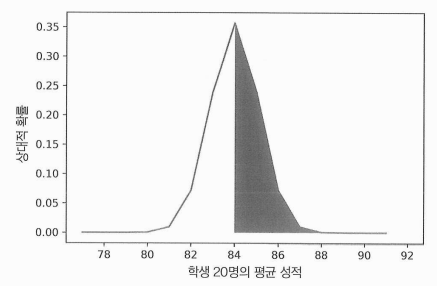
• 평균이 정규 곡선을 동일한 절반 두 개로 완벽히 나누기에 stats.norm.sf(0, mean, sem) 0.5가 될 것이라 예상한다.

 

 

 

assert stats.norm.sf(mean, mean, sem) == 0.5
estimated_area = np.trapz(normal_likelihoods[mean:])
print(f"평균을 초과하는 추정 면적은 {estimated_area} 입니다")

• np.trapz(normal_likelihoods[mean:])는 0.5에 가깝지만 완전히 같지는 않음.

 

 

 

 

area = stats.norm.sf(90, mean, sem)
print(f"20명의 학생이 시험에 합격할 확률은 {area} 입니다.")

 

• area = stats.norm.sf(90, mean, sem)를 실행했을 때 이 함수는 90%를 초과하는 값의 간격에 대한 영역을 반환한 것을 알 수 있다.

 

 

6.3.2 계산된 확률 해석하기

몇몇 데이터가 제공되지 않는 경우 최선을 다했지만 불확실성이 남아있을 수 있다.

통계학자들은 이런 경우, 제한된 기록에 의존해 중대한 결정을 내려야 하는 경우가 많다.

따라서 불완전한 정보에서 결론을 도출할 때는 매우 신중해야 한다.

 

 

 

 

7 주차 바로 보기

https://marble-shovel-9f2.notion.site/7-9-1c9cbc174299809da8d2da849d404a70?pvs=4